Public-Key Cryptography: Road to Bitcoin Smart Contracts #3
Objective
This article hopes to:
1) Investigate Public Curve Cryptography in a manner that is self-contained.
2) Explore cryptographic concepts and problems through visual aids without assuming advanced knowledge of the mathematics underlying the subject.
An Ode to the Bitcoin Abyss
“And if you gaze long enough into an abyss, the abyss will gaze back into you.”
Friedrich Nietzsche, Beyond Good and Evil
When you walk across a dark room to flip a light switch, you expect the light to turn on.
But can you explain why the light turns on?
Let’s go one step further: given enough resources, can you build a complex electrical system – power generation, transmission, and distribution – that enables a user to brighten a room at the flick of a switch?
Most of us do not sit and agonize over the amazing science and engineering that occurs behind the scenes when we use modern technology; we just flip the switch and carry on with our lives. Almost all of us do not have the current knowledge to recreate the systems that we use. This approach works for a vast majority of us for a vast majority of technologies: electricity, hydro, computing, mobile, vehicles, etc. Most of us do not care how the technology works, we just want to know that it works so that we can use it successfully.
Even individuals who would consider themselves “technologists” in some shape or form have a difficult time explaining the nature of a large number of tools they use on a daily basis. In fact, if someone was to point to a piece of technology and ask, “How does that work?”, we would have a half-ass explanation at best for almost all of the technologies that we use.
This approach works because it is so efficient: it would be extremely burdensome on us if we needed to know how every piece of technology works to use it. Knowledge specialization has allowed society to increase economic output steadily: if Alice is better at building cars relative to Bob, and Bob is better at building computers relative to Alice, the most efficient economic decision would be to specialize and trade goods.
You may be asking yourself: What does this have anything to do with Bitcoin Smart Contracts?
Bitcoin is an abyss whose lure strengthens as you delve deeper into its unknowns. While no one has reached the bottom of the Bitcoin abyss, those who delve deeper have a relative economic advantage compared to others. Let us provide two examples:
Caeteris paribus (All else being equal), those who conduct on-chain analytics alongside technical analysis have a better understanding of the Bitcoin market relative to those who only conduct technical analysis; thus, the former may be expected to have more accurate mid- to long-term price predictions.
Caeteris paribus, those who understand how to use Bitcoin hardware wallets have lesser counter-party risk relative to those who keep their keys on exchanges; thus, the former may be expected to have greater control over their coins.
We have all heard the cliché phrase knowledge is power. While we may never be able to deploy an end-to-end understanding of Bitcoin and its implications, those of us who try to have a deeper understanding of Bitcoin will have a relative economic advantage over those who do not.
With this in mind, those of us who have a deeper knowledge of Bitcoin Smart Contracts will have a relative economic advantage over those who do not. If you understand the technical underpinnings of Bitcoin Smart Contracts, you have a better understanding of this technology’s implications, strengths, and limitations. By better understanding its implications, strengths, and limitations, you can make decisions that are better informed and thus more accurate on average.
A following question may be: Well, aside from a relative economic advantage, why try so hard to understand the technical aspects of Bitcoin Smart Contracts?
The answer to this question is not obvious.
You can argue that the ability to interact with Bitcoin and Bitcoin Smart Contracts is vastly more important than the knowledge of its technical underpinnings. Like with all other technologies that we take for granted, it may be good enough to just hop on the Bitcoin train and stay along for the ride. There is a point to this frame of thinking. Many individuals may not care enough about the decision-making advantages that a technical understanding of Bitcoin brings into their lives to try and develop such an understanding.
How can we convince these people?
The answer may turn out to be that we can’t convince these people.
Bitcoin changes those who delve deeper into the abyss. Many people will not want to experience this change out of fear, greed, misunderstanding, or any other human emotion or rationalization.
If you are a curious individual who wants to desperately make sense of the technical and societal implications of Bitcoin Smart Contracts, continue down into the abyss.
If you are not ready or willing to enter, that is fine. This article will be here waiting for you to take the next step.
It may be intimidating to stare into the darkness of the abyss. As we look, the concepts and implications of Bitcoin and Bitcoin Smart Contracts that we neither understand nor appreciate challenge our unarticulated presuppositions and paradigms of thought.
It may be even more intimidating to enter the darkness, to try and make sense of Bitcoin and its implications. Those that enter the abyss may find themselves forever changed in an unpredictable manner.
Do not fear what you find in the abyss.
Do not fear if what you find changes you.
Whether it be technical notation or mathematical symbols that you do not understand, we will be here with you every step of the way to walk with you through the darkness.
Public-Key (Asymmetric) Cryptography
Review
As discussed in the last article in the Road to Bitcoin Smart Contracts series, Public-Key (Asymmetric) Cryptography does not require both parties, Alice and Bob, to share a secret key prior to exchanging messages. In Public-Key Cryptography, Alice has her own secret key and Bob has his own secret key. When combined together by some mathematical operation, these two private keys form the shared secret key. This method is called asymmetric as Alice and Bob have different levels of knowledge of the shared secret key.
General Setup
Bob and Alice do not share a secret key through a private channel.
Alice has her own secret key a.
Bob has his own secret key b.
Bob wants to send a plaintext message m to Alice in a secret manner so that an eavesdropper, Eve, cannot understand the message.
Bob enciphers the message with his secret key. I.e., the plaintext turns into ciphertext c.
Bob sends the ciphertext to Alice through a public channel.
After receiving the ciphertext, Alice applies her secret key to decipher the ciphertext into plaintext.
If the procedure is conducted properly, Eve cannot know the either Alice’s or Bob’s key, cannot guess their keys, or cannot convert the ciphertext to plaintext without knowing either one of their keys.
Throughout this article, we will answer the following question: if the two secret keys are different, how do we ensure that the plaintext that Bob receives is identical to the plaintext that Alice sent?
Importance of Public-Key Cryptography
Public-Key Cryptography enables 3 properties to emerge in digital space:
Non-repudiation – once she sends a message, Alice cannot falsely claim that she did not send it. Similarly, once he receives a message, Bob cannot falsely claim that he did not receive it.
Confidentiality – Bob alone can read Alice’s messages.
Authenticity – Alice can “sign” her messages to prove to Bob that only she could have sent it in a manner that prevents tampering from Eve.
Public-Key Cryptography is the foundation that most encryption schemes are built upon in modern computing and networking. Whether you are using email, social media, electronic payments, or electronic signatures, you are interacting in one way or another with Public-Key Cryptography. In fact, every time you use a secure connection over the internet via a VPN, you interact with Public-Key Cryptography.
In future articles concerning the Bitcoin protocol and Bitcoin Smart Contracts, we will explore several critical applications of Public-Key Cryptography.
Modular Arithmetic
An Introduction to Modular Arithmetic
Similar to the way that calculus contains building blocks that underpin psychical systems, modular arithmetic contains building blocks that make up Public-Key Cryptosystems.
In this section, we will explore modular arithmetic. Without a rudimentary knowledge of this subject, moving forward while maintaining a high level of understanding is frankly infeasible. Therefore, we must cover this (admittedly dry) material for readers unfamiliar with the topic.
For readers who are familiar with modular arithmetic, feel free to skip this section. For readers who wish to delve deeper into the mathematics of groups and fields – algebraic structures closely related to modular arithmetic – see the following:
Sections 1.3 – 1.5 in An Introduction to Mathematical Cryptography by Hoffstein 2014 [1]
Integers and Primes
Before delving into modular arithmetic, let us first remind ourselves of two very basic definitions:
Integers: numbers (whole numbers) that can be written without the use of fractions or decimals. In this article series, we will largely focus on the positive integers (0, 1, 2, 3, …).
Primes: integers that can only be divided by 1 or themselves. A few examples of small primes are 2, 3, 5, 7, 11, and 13.
Telling Time
What happens to the time on your smartphone as midnight approaches?
If you set your smartphone’s time to 24-hour (military time) instead of AM/PM, you will see that the time approaches 23:59 and then resets to 00:00 at midnight. If you struggle to interrupt military time, please read this short guide for a quick explanation (Military Time Chart).
Let us ignore minutes and just focus on the hours displayed in military time. If you were to stay up throughout an entire 24-hour period starting at midnight, you would see your smartphone display 0, 1, 2, 3, …, 22, and 23 until the next day began where again your smartphone would display 0. Focusing only on hours, there are 24 different types of units (in this case, integers or whole numbers) that can be displayed by your smartphone throughout an entire 24-hour period:
Z24 = {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23}
The symbol above denotes the set of Integers modulo 24. Do not let the scary name or notation fool you; when you are telling time (ignoring minutes) using a 24-hour clock, you are interacting with the set of Integers modulo 24. All this notation means is that there are 24 units (in this case, integers or whole numbers) that you can work with. If you were to add 23+1, it would be just like waiting an hour starting at 23: your smartphone would indicate that the time is 0.
Modular Addition
Telling time (ignoring minutes) using a 24-hour clock is an example of modular arithmetic that you are intimately familiar with; however, very few individuals are familiar with the symbolic notation. There is a power to identifying the name or definition of a thing or action which we will try to capture in the following example:
Let us now look at a wall clock that only displays hours with the 12 replaced by a 0. There are 12 units (integers) on this clock that denote the time in hours that range from 0 to 11:
If it is currently 1, what will be the time in 3 hours? This is trivial – it will be 4.
If it is currently 10, what will be the time in 3 hours? This is not difficult looking at the clock. You move 3 units clockwise from 10 until you land on the desired unit: 1.
What is going on here from a technical perspective? Integer additional modulo 12. Below is the set of integers modulo 12 that corresponds to our clock:
Z^12=0,1,2,3,4,5,6,7,8,9,10,11
If it is currently 1 and we want to know the time in 3 hours, we perform modular addition:
1+3 =4=4 mod 12
If its currently 10 and we want to know the time in 3 hours, we again perform modular addition:
10+3 =13=1 mod 12
The mod 12 part of this equation will be new to many of you. Do not fear, all mod indicates is the type of “clock” that you are working with. In this case, it is a clock with units 0 through 11 as above.
If we perform the following modular addition with a 24-hour “clock”:
22+3 =25 =1 mod 24
we see that the principles are the same.
Modular Addition (mod N):
Suppose you have two integers x and y the sum z (i.e., x + y = z). If you want to solve x + y = z mod N, construct a “clock” as above for size N.
Start at 0 and move around the clock in a clockwise direction x times. Where you land on the clock is x mod N.
Next, from x mod N, move along the clock in a clockwise direction y times. Where you land on the clock is x + y mod N = z mod N.
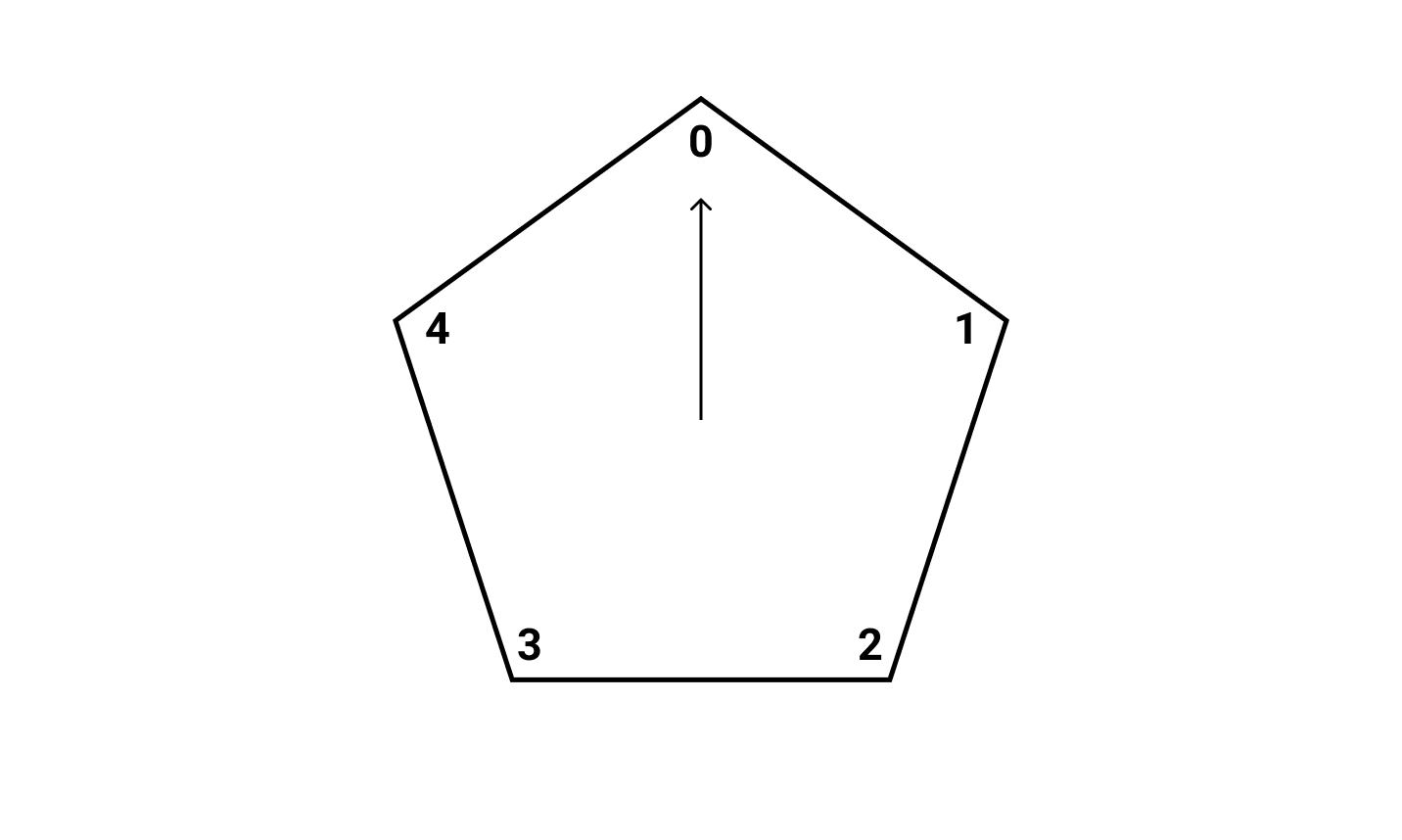
Let x = 9 and y = 3. We want to solve x + y = z mod N where N = 5.
First, construct a clock of size N = 5:
Second, starting from 0, move clockwise 9 times:
Third, starting from 4, move clockwise 3 times:
We have just performed modular addition:
x =9 =4 mod 5
y =3 =3 mod 5
x+y =9+3 =12=2 mod 5
Note: when performing modular arithmetic, it is sometimes easier to perform the calculations using standard arithmetic and then reduce the final answer by modulo N via a modulo calculator. For those who are following along with the calculations in this section, you can access a modulo calculator here.
Modular Subtraction
Let us now turn to modular subtraction.
Modular subtraction is very similar to modular addition with one caveat: we add in the counter-clockwise direction on our clock.
Modular Subtraction (mod N):
Suppose you have two integers x and y the difference z (i.e., x - y = z). If you want to solve x - y = z mod N, construct a “clock” for size N.
Start at 0 and move around the clock in a clockwise direction x times. Where you land on the clock is x mod N.
Next, from x mod N, move along the clock in a counter-clockwise direction y times. Where you land on the clock is x - y = z mod N.
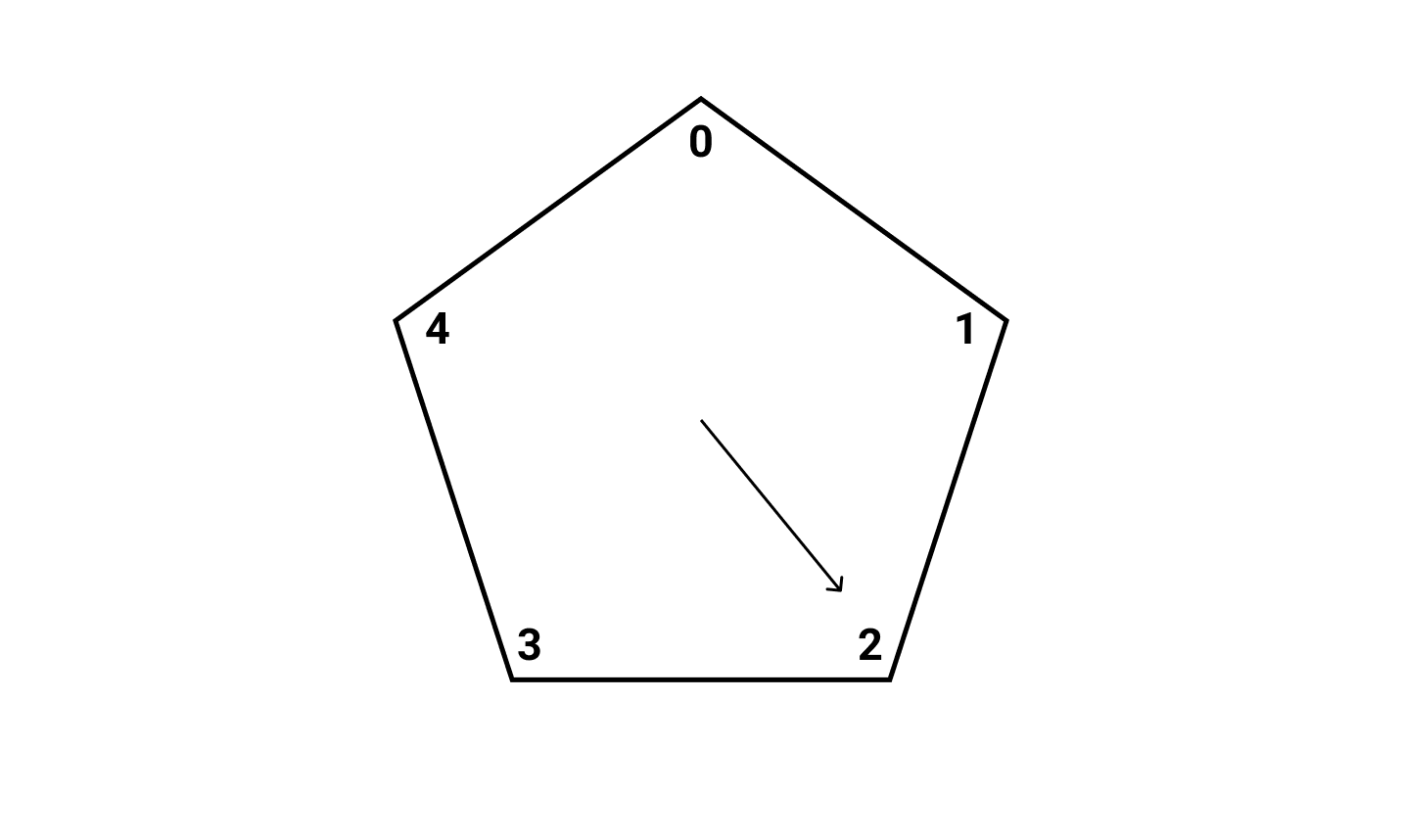
Let x = 9 and y = 3. We want to solve x - y = z mod N where N = 5.
First, construct a clock of size N = 5:
Second, starting from 0, move clockwise 9 times:
Third, starting from 4, move counter-clockwise 3 times:
You have arrived at the solution.
We have just performed modular subtraction:
x =9 =4 mod 5
y =3 =3 mod 5
x-y =9-3 =6=1 mod 5
Modular Multiplication
Let us now turn to modular multiplication:
Modular Multiplication: Let x, y, and z be integers modulo N. We define modular multiplication to be the arithmetic:
xy = z mod N
Modular multiplication, like the regular multiplication that you are used to, is basically repeated addition.
Let x = 9 and y = 3. We want to solve xy = z mod N where N = 5.
First, construct a clock of size N = 5:
Second, starting from 0, move clockwise 9 times:
Third, starting from 4, move clockwise 9 times:
Fourth, starting from 3, move clockwise 9 times:
You have arrived at the solution.
We have just performed modular multiplication:
x =9 =4 mod 5
y =3 =3 mod 5
xy=93=27=2 mod 5
Modular Multiplicative Inverses
Let us now turn to find a modular multiplicative inverse – the equivalent of division in modular arithmetic.
First, we will introduce a concept known as the Greatest Common Divisor:
Greatest Common Divisor (gcd): Let x and y be integers. The Greatest Common Divisor of x and y (denoted gcd(x,y)) is the largest number that divides both x and y.
Example: What is gcd(6,3)?
A naïve method to solve this example would be to find all the numbers that divide 6 and all the numbers that divide 3 and compare:
Factors (Divisors) of 6: 1,2,3,6
Factors of 3: 1,3
We have a match: gcd(6,3) = 3.
There are faster algorithms to find the gcd of two or more integers; one algorithm that is commonly used is the Euclidean Algorithm.
Returning to modular multiplicative inverses:
Modular Multiplicative Inverse: Let x and y be integers modulo N. If xy = 1 mod N, then y is the modular multiplicative inverse of x and vice-versa. Furthermore, x has a modular multiplicative inverse if and only if gcd(x,N) = 1. In most applications of cryptography, N = p prime so gcd(x,N) = 1 holds true.
Example: What is the modular multiplicative inverse of 2 mod 5?
First, let’s check if 2 mod 5 has a modular multiplicative inverse:
Factors of 2: 1,2
Factors of 5: 1,5
gcd(2,5) = 1
Great! 2 has a modular multiplicative inverse! Now let’s find it by naïve trial and error:
2(1) = 2 = 2 mod 5
2(2) = 4 = 4 mod 5
2(3) = 6 = 1 mod 5
Awesome! The modular multiplicative inverse of 2 mod 5 is 3 mod 5 as 2(3) mod 5 = 1 mod 5!
A common notation that we will use for multiplicative modular inverses is as follows:
which is equivalent to:
xy = 1 mod N
For those who are closely following along with the arithmetic, you can find a modular multiplicative inverse calculator here.
Modular Exponentiation
Let us now turn to modular exponentiation. Similar to typical exponentiation, modular exponentiation can be understood as repeated modular multiplication.
Modular Exponentiation: Let x, y, and z be integers modulo N. We define modular exponentiation to be the arithmetic:
x y = z mod N
Let x = 9 and y = 3. We want to solve x y = z mod N where N = 5.
First, construct a clock of size N = 5:
Second, rewrite the exponentiation as repeated multiplication for simplicity:
9^3 = 9(9)(9) = 729
Third, perform modular multiplication to arrive at the solution:
We have just performed modular multiplication:
x =9 =4 mod 5
y =3 =3 mod 5
Let us now define multiplicative order – an extension of modular exponentiation that is used heavily in the following section:
Multiplicative Order: Let x be an integer modulo N. We define the multiplicative order of x to be the integer n such that:
If x = 3 and N = 5, what is the multiplicative order of x? Let us find n by naïve trial and error:
x1 = 3 = 3 mod 5
x2 = 9 = 4 mod 5
x3 = 27 = 2 mod 5
x4 = 81 = 1 mod 5
So, x has a multiplicative order of 4!
Multiplicative order leads us to the final tool that we will need to construct the Discrete Log Problem:
Primitive Root of p: Let p be a prime. We define a primitive root of p to be an integer x modulo p such that the multiplicative order of x is (p – 1):
In our previous example, x = 3 and p = 5.
So, 3 is a primitive root of 5:
Discrete Log Problem
For the mathematically inclined, the next sections correspond with the following:
Sections 2.2 – 2.4 in An Introduction to Mathematical Cryptography by Hoffstein 2014 [1]
Return of Trapdoor Functions
In the second article of the Road to Bitcoin Smart Contracts series, we introduced the notion of trapdoor functions. It is in this section that the concept of trapdoor functions makes a return through the Discrete Log Problem.
Reviewing the previous section of this article, we know modular exponentiation has the form:
Suppose we know x = 3, z = 5, and N = 17:
How hard is it to find y?
It turns out that for this example, y = 5 and is not that difficult to find by plugging in numbers from 0 to 16.
However, in general, finding y is extremely difficult for very large numbers. It is this computational difficulty that underpins the Discrete Log Problem.
Of course, if you know y it is very easy to check as modular exponentiation is very fast using a modern computer. The “trapdoor” in this setup is knowledge about y and its properties. The more you know about y, the easier it is to solve the aforementioned equation.
Discrete Log Problem
To construct the Discrete Log Problem, we must use the following tools that were defined in the previous section:
Integers
Primes
Modular Exponentiation
Multiplicative Order
Primitive Roots
Discrete Log Problem: Let x be a primitive root of a prime p. Let z be a positive integer modulo p. The Discrete Logarithm Problem (DLP) is the mathematical problem of finding an integer y such that:
Attacks
If constructed properly (i.e., large, carefully chosen integers), the DLP is extremely difficult to solve for modern computers. We will not spend a lot of time focusing on potential attacks in this article; instead, we will link a few contemporary generic attacks on the DLP for those who would like to learn more:
Diffie-Helman Key Exchange
Diffie-Helman Key Exchange
In 1976, Diffie and Hellman created the first Public-Key protocol: the Diffie-Helman Key Exchange. This cryptographic protocol uses the same tools that we set up in the previous section on the DLP to create an ingenious method to exchange secret keys across public channels.
Throughout this article, we are focusing on exploring the question: if the two secret keys are different in Public-Key Cryptography, how do we ensure that the plaintext that Bob receives is identical to the plaintext that Alice sent?
The Diffie-Helman Key Exchange provides an answer to this question: Alice and Bob can create a shared key without exposing their either of their private keys to Eve or to the other individual.
You may be asking yourself: What the hell does that mean?
Well, let us examine the setup of the Diffie-Helman Key Exchange:
Creation of Public Parameters
Bob and Alice do not share a secret key through a private channel.
Alice or Bob chooses and publishes a (large) prime p and a primitive root g mod p. These two values are public and shared by Alice and Bob.
First Private Computations
- Alice chooses her own secret key a.
- Bob chooses his own secret key b.
- Alice computes A = g a mod p.
- Bob computes B = g b mod p.
Public Exchange
7. Alice sends A to Bob via a public channel.
8. Bob sends B to Alice via a public channel.
Second Private Computations
Alice computes Ba mod p.
Bob computes Ab mod p.
By the properties of modular exponentiation, C = Ab mod p = Ba mod p. So, C is their shared secret key that they can use in further computations without exposing a or b.
To see that Ab mod p = Ba mod p, notice that Ab = (ga)b = (gab) = (gb)a = Ba mod p by the properties of modular exponentiation.
The security of this protocol relies on the difficulty on solving the DLP. An attacker knows p, g, A, and B. To find Alice’s or Bob’s secret keys, they would have to solve the DLP:
Solve for a for A = ga mod p (Alice’s Secret Key)
Solve for b for B = gb mod p (Bob’s Secret Key)
If the appropriate integers are chosen, this setup is extremely difficult for even modern supercomputers to break.
We will construct an (very insecure) example with small numbers to demonstrate the utility of the Diffie-Helman Key Exchange:
Creation of Public Parameters
Alice and Bob agree to use the fowling public parameters (g, p) = (2, 13).
First Private Computations
Alice chooses her secret key a = 3 and computes A = ga mod p = 8 mod 13.
Bob chooses his secret key b = 7 and computes B = gb mod p = 11 mod 13.
Public Exchange
Alice sends A to Bob, while Bob sends B to Alice.
Second Private Computations
Alice computes C = Ba mod p = 5 mod 13.
Bob computes C = Ab mod p = 5 mod 13.
Elgamal Public-Key Cryptosystem
Elgamal: A Functional Public Key Cryptosystem
While the Diffie-Helman Key Exchange protocol allows Alice and Bob to share secret keys without exposing their own private keys, it does not allow for the exchange of full messages (which is ultimately what we want from a cryptosystem).
However, in 1985, Elgamal described a new cryptosystem based on the DLP and the Diffie-Helman Key Exchange that finally addressed this issue.
Let us now examine the setup of the Elgamal Public-Key Cryptosystem:
Creation of Public Parameters
Bob and Alice do not share a secret key through a private channel.
Alice or Bob chooses and publishes a (large) prime p and a primitive root g mod p. These two values are public and shared by Alice and Bob.
Alice: Key Creation
Alice chooses her own secret key a where a is greater than (or equal to) 0 but less than (or equal to) p – 1.
Alice computes A = ga mod p.
Alice sends A to Bob.
Bob: Encryption
Bob chooses a plaintext message m along with random integer k.
Bob computes d = gk mod p and e = mAk mod p.
Bob sends d and e to Alice via a public channel.
Alice: Decryption
- Alice computes (da)-1 (e) mod p = m.
Again, the security of this cryptosystem relies on the difficulty on solving the DLP. An attacker knows p, g, A, d, and e. While the security of the Elgamal Cryptosystem is more complex than Diffie-Helman, it is still secure given the appropriate selection of integers.
We will construct an (very insecure) example with small numbers to demonstrate the utility of the Elgamal Public-Key Cryptosystem:
Creation of Public Parameters
Alice and Bob agree to use the fowling public parameters (g, p) = (2 , 13).
Alice: Key Creation
Alice chooses her secret key a = 3 and computes A = ga mod p = 8 mod 13.
Alice sends A to Bob.
Bob: Encryption
Bob selects plaintext m = 10 mod 13.
Bob selects random integer k = 6.
Bob computes d = gk mod p = 12 mod 13.
Bob computes e = mAk mod p = 3 mod 13.
Bob sends d and e to Alice.
Alice: Decryption
Alice computes (da)-1 (e) mod p = (12)(3) = 36 = 10 mod 13 = m.
First Steps
If you have made it this far, congratulations and thank you! You have taken steps further into the Bitcoin abyss.
While the first two articles in this series were largely conceptual in nature, this article is the first to introduce hints of advanced mathematics typically taught at the sophomore undergraduate level. The next few articles will contain much more advanced mathematics as we explore Elliptic Curve Cryptography – the cryptosystem that underlies the Bitcoin protocol.
As stated at the beginning of this article:
Do not fear what you find in the abyss.
Do not fear if what you find changes you.
Whether it be technical notation or mathematical symbols that you do not understand, we will be here with you every step of the way to walk with you through the darkness.
Acknowledgements
I want to thank Mason Jappa, Sam Chwarzynski, Tanner Davis and the Blockware Solutions Team for their continued support and valuable feedback on drafts of this series of articles.
Disclaimer
The views presented in this article as well as any errors are my own. If you think that any section of this article requires technical revision, please email me at mateusz@blockwaresolutions.com.
This article is for informational purposes only. It is not intended to be investment advice. Contact a licensed professional for investment advice.
Contact
Mateusz (Matthew) Faltyn
Blockchain Developer | Blockware Solutions LLC
Bitcoin Pool Operator | mine . blockwarepool . com
Proprietary Research | Sign up for our newsletter on our website
Follow us on Twitter | @FaltynMateusz @BlockwareTeam
Join our Telegram Group | BlockwareSolutionsOfferings
References
1. Hoffstein J, Pipher J, Silverman JH. An Introduction to Mathematical Cryptography. 2nd ed. New York: Springer-Verlag New York; 2014. doi:10.1007/978-1-4939-1711-2_1